图的遍历

深度优先遍历

• 深度优先遍历(Depth First Search),也称为深度优先搜索,简称DFS

• 它的具体思是:无论从哪个定点开始都可以遍历所有顶点

• 现在要遍历这样一个图:

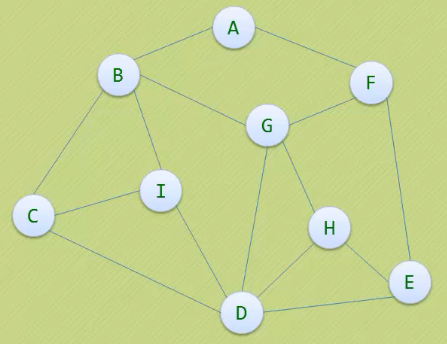
• 我们约定右手原则:在没有碰到重复顶点的情况下,分叉路口始终是向右手边走,没路过一个顶点就做一个记号

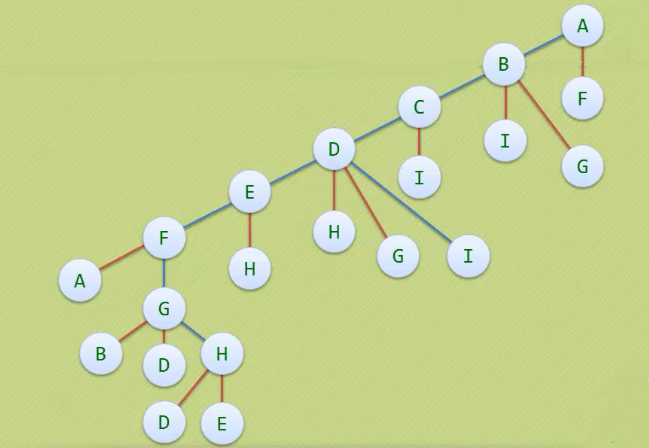
• 我们走过的路就是对这颗蓝色的树进行前序遍历!

马踏棋盘算法

• 马踏棋盘问题(又称骑士周游或骑士漫游问题)是算法设计的经典问题之一

• 国际象棋的棋盘为8*8的方格棋盘,现将"马"放在任意指定的方格中,按照"马"走棋的规则将"马"进行移动.要求每个方格只能进入一次,最终使得"马"走遍棋盘64个方格

• 要求用1-64来标注"马"移动的路径

• 最多搜索8^64次

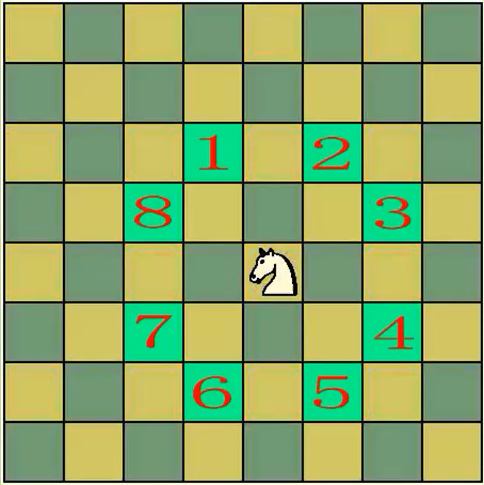
• 一些相关知识点

  • 回溯法

    思想很简单,就是一条路走到黑,碰壁了再回来一条路走到黑......一般和递归还有深度优先搜索(DFS)可以很好的搭配使用

  • 哈密尔顿路径:

    哈密尔顿路径是指经过图中的每个顶点,且只经过一次的一条轨迹.如果这条轨迹是一条闭合的路径(从起点出发不重复的遍历所有点后仍能回到起始点),那么这条路径称为哈密尔顿路径

Code

#include <stdio.h>
#include <time.h>

#define X 8
#define Y 8

int chess[X][Y];

//找到基于(x,y)位置的下一个可走的位置
int nextxy(int *x,int *y,int count)
{
    switch(count)
    {
    case 0:
        if(*x+2 <= X-1 && *y-1 >= 0 && chess[*x+2][*y-1]==0)
        {
            *x = *x + 2;
            *y = *y - 1;
            return 1;
        }
        break;

    case 1:
        if(*x+2 <= X-1 && *y+1 <= Y-1 && chess[*x+2][*y+1]==0)
        {
            *x = *x + 2;
            *y = *y + 1;
            return 1;
        }
        break;
    case 2:
        if(*x+1 <= X-1 && *y-2 >= 0 && chess[*x+1][*y-2]==0)
        {
            *x = *x + 1;
            *y = *y - 2;
            return 1;
        }
        break;

    case 3:
        if(*x+1 <=X-1 && *y+2 <= Y-1 && chess[*x+1][*y+2]==0)
        {
            *x = *x + 1;
            *y = *y + 2;
            return 1;
        }
        break;

    case 4:
        if(*x-2 >= 0 && *y-1 >= 0 && chess[*x-2][*y-1]==0)
        {
            *x = *x - 2;
            *y = *y - 1;
            return 1;
        }
        break;

    case 5:
        if(*x-2 >= 0 && *y+1 <= Y-1 && chess[*x-2][*y+1]==0)
        {
            *x = *x - 2;
            *y = *y + 1;
            return 1;
        }
        break;

    case 6:
        if(*x-1 >= 0 && *y-2 >= 0 && chess[*x-1][*y-2]==0)
        {
            *x = *x - 1;
            *y = *y - 2;
            return 1;
        }
        break;

    case 7:
        if(*x-1 >= 0 && *y+2 <= Y-1 && chess[*x-1][*y+2]==0)
        {
            *x = *x - 1;
            *y = *y + 2;
            return 1;
        }
        break;

    default:
        break;

    }
    return 0;
}

void print()
{
    int i,j;

    for(i=0;i<X;i++)
    {
        for(j=0;j<Y;j++)
        {
            printf("%2d\t",chess[i][j]);
        }
        printf("\n");
    }
    printf("\n");
}

//深度优先遍历棋盘
//(x,y)为位置坐标
//tag是标记遍历.每走一次,tag+1
int TravelChessBoard(int x,int y,int tag)
{
    int x1 = x,y1 = y, flag = 0, count = 0;
    chess[x][y] = tag;

    if(X*Y==tag)
    {
        print();
        return 1;
    }

    //找到马的下一个可走的坐标(x1,y1),如果找到flag=1.否则为0
    flag = nextxy(&x1,&y1,count);
    while(0==flag && count<7)
    {
        count++;
        flag = nextxy(&x1,&y1,count);
    }

    while(flag)
    {
        if(TravelChessBoard(x1,y1,tag+1))
        {
            return 1;
        }

        //继续找到马的下一步可走的坐标(x1,y1),如果找到flag=1.否则为0
        x1 = x;
        y1 = y;
        count++;

        flag = nextxy(&x1,&y1,count);
        while(0==flag && count<7)
        {
            count++;
            flag = nextxy(&x1,&y1,count);
        }
    }

    if(0 == flag)
    {
        chess[x][y] = 0;
    }
    return 0;
}

int main()
{
    int i,j;
    clock_t start,finish;

    start = clock();

    for(i=0;i<X;i++)
    {
        for(j=0;j<Y;j++)
        {
            chess[i][j]=0;
        }
    }

    if(!TravelChessBoard(2,0,1))
    {
        printf("马踏棋盘是失败!");
    }
    finish = clock();
    printf("\n本次耗时: %f秒\n\n",(double)(finish-start)/CLOCKS_PER_SEC);
    return 0;
}

广度优先搜索

• 广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS

• 图的广度优先类似于树的层次遍历

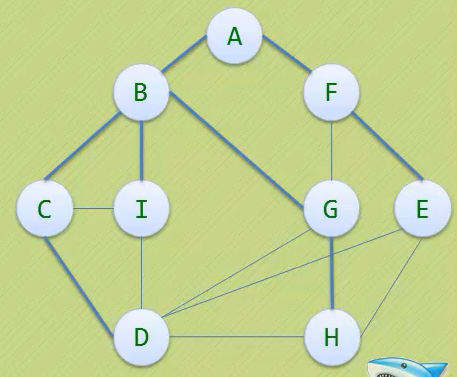
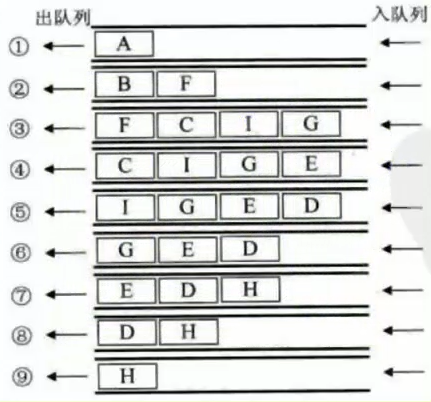
• 要实现对图的广度优先遍历,我们可以利用队列来实现

• 邻接矩阵的广度优先遍历思路

  从一个顶点开始,将其入队列,将它连接的节点入队列,将它弹出队列,后面依次这样做

//邻接矩阵的广度遍历算法(代码没有验证)

void BFSTraverse(MGraph G)
{
    int i,j;
    Queue Q;

    for(i=0;i<G.numVertexes;i++)
    {
        visited[i] = FALSE;
    }

    initQueue(&Q);

    for(i=0;i<G.numVertexes;i++)
    {
        if(!visited[i])
        {
            printf("%c ",G.vex[i]);
            visited[i] = TRUE;
            EnQueue(&Q,i);

            while(!QueueEmpty(Q))
            {
                Deque(&Q,&i);
                for(j=0;j<G.numVertexes;j++)
                {
                    if(G.art[i][j]==1 && !visited[j])
                    {
                        printf("%c ",G.vex[j]);
                        visited[j] = TRUE;
                        EnQueue(&Q,j);
                    }
                }
            }
        }
    }
}

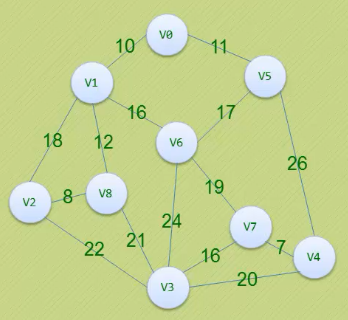
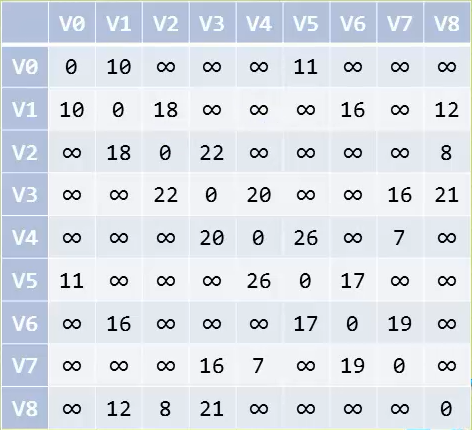
最小生成树-普里姆(Prim)算法

void MiniSpanTree_Prim(MGraph G)
{
    int min,i,j,k;
    int adjvex[MAXVEX];     //保存相关顶点下标
    int lowcost[MAXVEX];    //保存相关顶点间边的值

    lowcost[0] = 0;     //V0作为最小生成树的根开始遍历,权值为0
    adjvex[0] = 0;      //V0第一个加入

    //初始化操作
    for(i=1;i<G.numVertexes;i++)
    {
        lowcost[i] = G.arc[0][i];   //将邻接矩阵第0行所有权值先加入数组
        adjvex[[i] = 0;     //初始化全部先为V0的下标
    }

    //真正构造最小生成树的过程
    for(i=1;i<G.numVertexes;i++)
    {
        min = INFINITY;     //初始化最小权值为65535等不可能数值
        j = 1;
        k = 0;

        //遍历全部顶点
        while(j < G.numVertexes)
        {
            //找出lowcost数组已存储的最小权值
            if(lowcost[j]!=0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;  //将发现的最小权值的下标存入k,以待使用
            }
            j++;
        }

        //打印当前顶点边中权值最小的边
        printf("(%d,%d)",adjvex[k],k);
        lowcost[k] = 0;     //将当前顶点的权值这只为0,表示此顶点已经完成任务,进行下一个顶点的遍历

        //邻接矩阵k行逐个遍历全部顶点
        for(j=1;j<G.numVertexes;j++)
        {
            if(lowcost[j]!=0 && G.arc[k][j]<lowcost[j])
            {
                lowcost[j] = C.arc[k][j];
                adjvex[j] = k;
            }
        }
    }
}

最小生成树-克鲁斯卡尔(Kruskal)算法

• 无论是普里姆算法还是克鲁斯卡尔算法,他们考虑问题的出发点都是:为使生成树上边的权值之和达到最小,则应使生成树中每一条边的权值尽可能的小

*　普里姆算法是以某顶点为起点，逐步找各个顶点上最小权值的边来构建最小生成树的

• 克鲁斯卡尔算法的思想是直接去找最小权值的边来构建生成树

• 边集数组

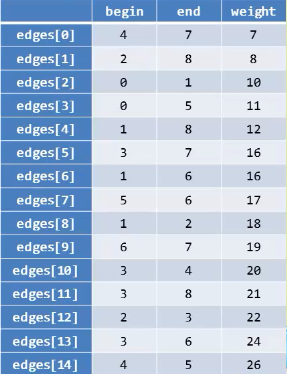
• Code

int Find(int *parent,int f)
{
    while(parent[f] > 0)
    {
        f = parent[f];
    }
    return f;
}

void MiniSpanTree_Kruskal(MGraph G)
{
    int i,n,m;
    Edge edges[MAGEDGE];    //定义边集数组
    int parent[MAXVEX];     //定义parent数组用来判断边与边是否形成环路

    for(i=0;i<G.numVertexes;i++)
    {
        parent[i] = 0;
    }

    for(i=0;i<G.numEdges;i++)
    {
        n = Find(parent,edges[i].begin);
        m = Find(parent,edges[i].end);

        if(n!=m)    //如果n==m,则形成环路,不满足
        {
            parent[n] = m;  //将此边的结尾顶点放入下标为起点的parent数组中,表示此顶点已经在生成树集合中
            printf("(%d,%d) %d ",edges[i].begin,edges[i].end,edges[i].weight);
        }
    }
}

• 最后的parent数组

• 当一个图边数少时克鲁斯卡尔算法效率会比较高,也就是说对稀疏图有很大优势;当一个图顶点数多时普里姆算法效率会比较高,也就是说对稠密图有很大优势

最短路径-迪杰斯特拉(Dijkstra)算法

• 在网图和非网图中,最短路径的含义是不同的

  • 网图是两顶点经过的边上权值之和最少的路径

  • 非网图是两顶点之间经过的边数最少的路径

  • 其实非网图就是权值都为1的网图

• 我们把路径起始的第一个顶点称为源点,最后一个顶点称为终点

• 求v0到v8的最短路径

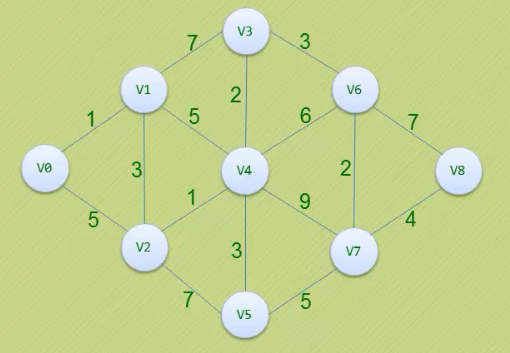
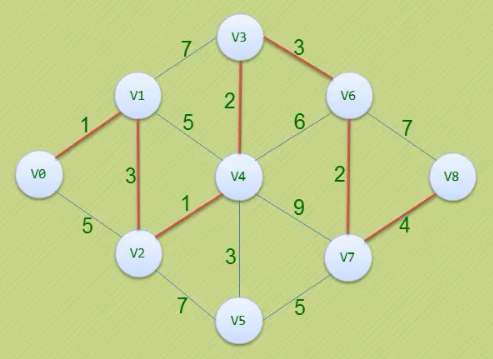
• 它并不是一下子就求出了v0到v8的最短路径,而是一步步求出它们之间顶点的最短路径,过程中都是基于已经求出的最短路径的基础上,求得更远顶点的最短路径

最短路径-弗洛伊德(Floyd)算法

• 迪杰斯特拉算法的时间复杂度为O(n^2),弗洛伊德算法的时间复杂度为O(n^3)

• 迪杰斯特拉算法求得是一个顶点到所有顶点的最短路径,弗洛伊德算法求得是所有顶点到所有顶点的最短路径

• P数组用来存储前驱结点

• D10=min{D00,D00+D1}

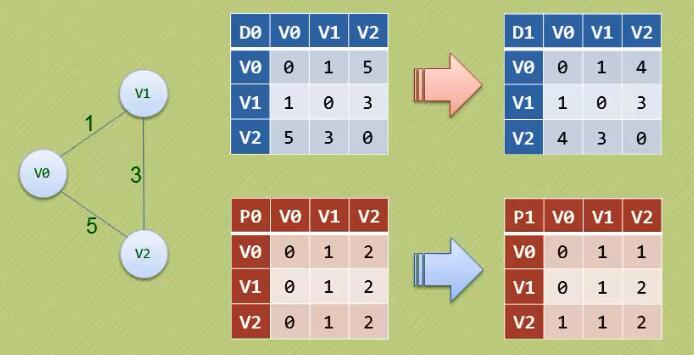
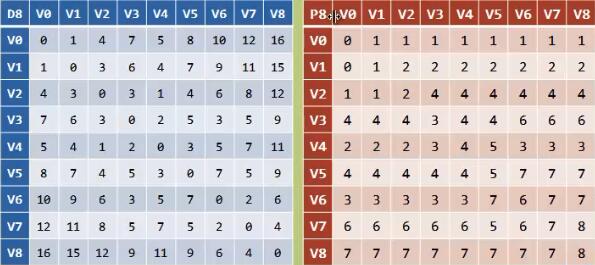
#define MAXEX 9
#define INFINITY 65535

typedef int Pathmatrix[MAXEX][MAXEX];
typedef int ShortestPathTable[MAXEX][MAXEX];

void ShortestPath_Floyd(MGraph G,Pathmatrix *p,ShortestPathTable *D)
{
    int v,w,k;
    //初始化D和P
    for(v=0;v<G.numVertexes;v++)
    {
        for(w=0;w<G.numVertexes;w++)
        {
            (*D)[v][w] = G.matrix[v][w];
            (*P)[v][w] = w;
        }
    }

    for(k=0;k<G.numVertexes;k++)
    {
        for(v=0;v<G.numVertexes;v++)
        {
            for(w=0;w<G.numVertexes;w++)
            {
                if((*D)[v][w] > (*D)[v][k] + (*D)[k][w])
                {
                    (*D)[v][w] = (*D)[v][k] + (*D)[k][w];
                    (*P)[v][w] = (*P)[v][k];
                }
            }
        }
    }
}

拓扑排序

• 一个有向无环图称为无环图(Directed Acyclic Graph),简称DAG图

• 所有的工程或者某种流程都可以分为若干个小的工程或者阶段,我们称这些小的工程或阶段为"活动"

• 在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,我们称之为AOV网(Active On Vertex Network)

• AOV网中的弧表示活动之间存在的某种制约关系

• AOV网不能存在回路!

• 拓扑序列:设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列V1,V2,......,Vn满足若从顶点Vi到Vj有一条路径,则再顶点序列中顶点vi必在顶点vj之前.则我们称这样的顶点序列为一个拓扑序列

• 拓扑排序:所谓的拓扑排序,其实就是对一个有向图构造拓扑序列的过程

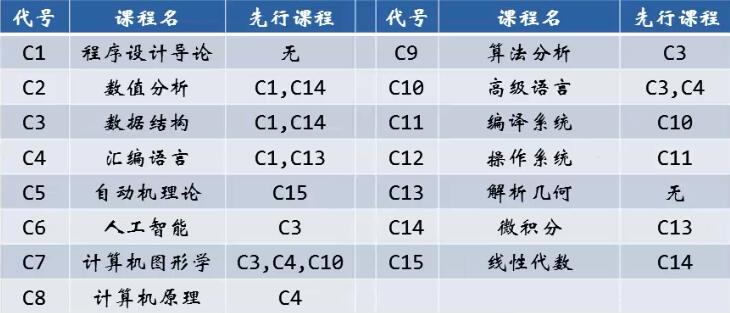
• AOV网图

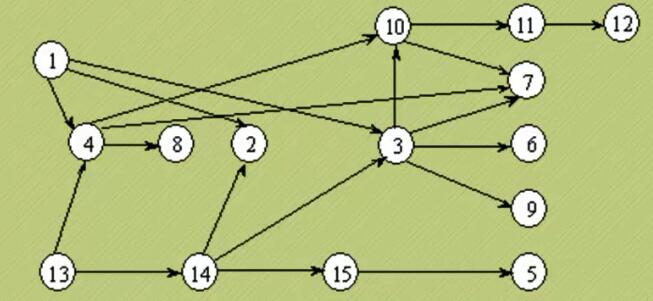
• 其中一种拓扑序列:1,13,4,8,14,15,5,2,3,10,11,12,7,6,9

• 对AOV网进行拓扑排序的方法和步骤如下:

  • 从AOV网中选择一个没有前驱的结点(该节点的入度为0)并且输出它

  • 从网中删除该点,并且删除从该点出发的全部有向变

  • 重复上述两步,知道剩余网中不再存在没有前驱的顶点为止

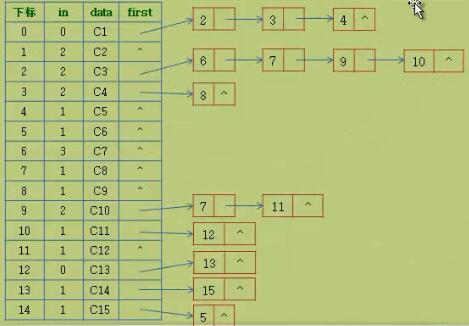
• code

//边表结点声明
typedef struct EdgeNode
{
    int adjvex;
    struct EdgeNode *next;
}EdgeNode;

//顶点表结点声明
typedef struct VertexNode
{
    int in;
    int data;
    EdgeNode *firstdege;
}VertexNode,AdjList[MAXVEX];

typedef struct
{
    AdjList adjList;
    int numVertexes,numEdges;
}graphAdjList,*GraphAdjList;

//拓扑排序算法
//若GL无回路,则输出拓扑排序序列并返回OK,否则返回ERROR
Satus TopologcalSort(GraphAdjList GL)
{
    EdgeNode *e;
    int i,k,gettop;
    int top = 0;//用于栈指针下标索引
    int count = 0;//用于统计输出顶点的个数
    int *stack; //用于存储入度为0的顶点

    stack = (int*)malloc(GL->numVertexes*sizeof(int));
    for(i=0;i<GL->numVertexes;i++)
    {
        if(0==GL->adjList[i].in)
        {
            stack[++top] = i;
        }
    }

    while(0!=top)
    {
        gettop = stack[top--];出栈
        printf("%d-> ",GL->adjList[gettop].data);
        count++;

        for(e=GL->adjList[gettop].firstdege;e;e=e->next)
        {
            k = e->adjvex;
            //将k号顶点邻接点的入度置为-1,因为他们的前驱已经消除
            //接着判断-1后入度是否为0,如果为0则也入栈
            if(!(--GL->adjList[k].in))
            {
                stack[++top] = k;
            }
        }
    }

    if(count<GL->numVertexes)
    {
        return ERROR;
    }
}

• 算法时间复杂度

  • 对一个具有n个顶点,e条边的网来说,初始建立入度为零的顶点栈,要检查所有顶点一次,执行时间为O(n)

  • 排序中,若AOV网无回路,则每个顶点入,出栈各一次,每个表结点被检查一次,因而执行时间为O(n+e)

  • 所以,整个算法的时间复杂度为O(n+e)

关键路径

• AOE网:在一个表示工程的带权有向图中,用顶点表示事件,用又向边表示活动,用边上的权值表示活动的持续时间,这种有向图的表示活动的网,我们称之为AOE网(Activity On Edge Network)

• 我们把AOE网中没有入边的顶点称为始点或源点,没有出边的顶点称为终点或汇点

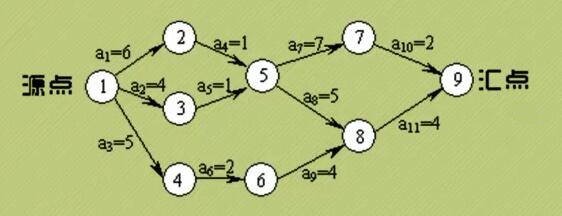
• AOV没有权值,AOE有权值