数据结构与算法之: 查找 第一部分 (九)
静态查找和动态查找
-
静态查找:数据集合稳定,不需要添加,删除元素的查找操作
-
动态查找:数据集合在查找的过程中需要同时添加或删除元素的查找操作
-
对于静态查找来说,我们不妨可以用线性表结构组织数据,这样可以使用顺序查找算法,如果我们再对关键字进行排序,则可以使用折半查找算法或斐波那契查找算法等来提高查找的效率
-
对于动态查找来说,我们则可以考虑使用二叉排序树的查找技术,另外我们还可以使用散列表结构来解决一些查找问题
顺序查找
- 顺序查找又叫做线性查找,是最基本的查找技术,它的查找过程是:从第一个(或最后一个)记录开始,逐个进行记录的关键字和给定值进行比较,若某个记录的关键字和给定值相等,则查找成功.如果查找了所有记录仍然找不到与给定值相对的关键字,则查找不成功
折半查找
-
如果待查找的记录是有序的,可以用折半查找
-
折半查找的基本思想:减小查找序列的长度,分而治之的进行关键字的查找
-
折半查找的实现过程:先确定待查找记录的所在范围,然后逐渐缩小这个范围,查找到该记录或查找失败为止
-
Code
int bin_search(int str[],int n,int key)
{
int low,high,mid;
low = 0;
high = n - 1;
while(low <= high)
{
mid = (low + high)/2;
if(str[mid] == key)
{
return mid;
}
if(str[mid]<key)
{
low = mid + 1;
}
if(str[mid] > key)
{
high = mid - 1;
}
}
return -1;
}- 复杂度O(log2n)
插值查找(按比例查找)
-
插值查找就像在查字典的时候,如果单词以a开头,一定会去前面找
-
如果数据变化的比较均匀,差值查找的效率比折半查找的效率高很多,如果不均匀可能会比折半查找慢很多
-
Code
-
Code
int bin_search(int str[],int n,int key)
{
int low,high,mid;
low = 0;
high = n - 1;
while(low <= high)
{
mid = low + (key-a[low]/(a[high]-a[low])*(high-low));
if(str[mid] == key)
{
return mid;
}
if(str[mid]<key)
{
low = mid + 1;
}
if(str[mid] > key)
{
high = mid - 1;
}
}
return -1;
}斐波那契查找(黄金分割查找)
-
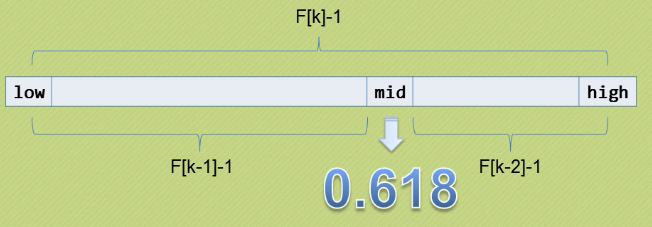
黄金比例 0.618:1
-
斐波那契数列(F[k]):1 1 2 3 5 8 13 21 34 55 89 ......
-
比例越来越接近0.612
- Code
#include <stdio.h>
#include <stdlib.h>
#define MAXN 20
/*
*产生斐波那契数列
* */
void Fibonacci(int *f)
{
int i;
f[0] = 1;
f[1] = 1;
for (i = 2; i < MAXN; ++i)
f[i] = f[i - 2] + f[i - 1];
}
/*
* 查找
* */
int Fibonacci_Search(int *a, int key, int n)
{
int i, low = 0, high = n - 1;
int mid = 0;
int k = 0;
int F[MAXN];
Fibonacci(F);
while (n > F[k] - 1) //计算出n在斐波那契中的数列
++k;
for (i = n; i < F[k] - 1; ++i) //把数组补全
a[i] = a[high];
while (low <= high)
{
mid = low + F[k - 1] - 1; //根据斐波那契数列进行黄金分割
if (a[mid] > key)
{
high = mid - 1;
k = k - 1;
}
else if (a[mid] < key)
{
low = mid + 1;
k = k - 2;
}
else
{
if (mid <= high) //如果为真则找到相应的位置
return mid;
else
return -1;
}
}
return 0;
}
int main()
{
int a[MAXN] = { 5, 15, 19, 20, 25, 31, 38, 41, 45, 49, 52, 55, 57 };
int k, res = 0;
printf("请输入要查找的数字:\n");
scanf("%d", &k);
res = Fibonacci_Search(a, k, 13);
if (res != -1)
printf("在数组的第%d个位置找到元素:%d\n", res + 1, k);
else
printf("未在数组中找到元素:%d\n", k);
return 0;
}线性索引查找
-
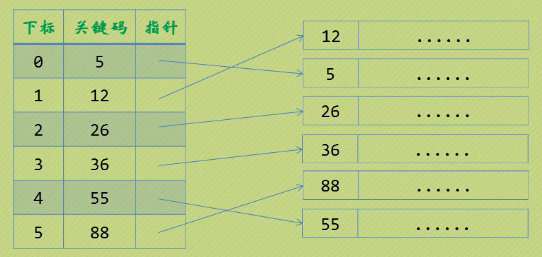
稠密索引
-
建立和\相同大小的索引表
-
应用于数据量比较小的,如果数据量比较大就必须放在硬盘上,增加了io
-
-
分块索引
- 块内无序,块间有序
-
倒排索引
二叉排序树
-
无序的顺序表在删除表中的元素的时候可以把后面的元素覆盖待删除的元素,这样效率较高
-
构建二叉排序树:小于根节点的放在左面,大于根节点的放在右边
-
二叉排序树(Binary Sort Tree)又称为二叉查找树,它或者是一颗空树,或者是具有下列性质死亡二叉树:
-
若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值
-
若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值
-
它的左,右子树也分别为二叉排序树(递归)
-
-
Code
//二叉树的二叉链表结点结构定义
typedef struct BiTNode
{
int data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;//递归查找二叉排序树 T 中是否存在 key
//指针f指向T的双亲,其初始值调用值为NULL
//若查找成功,则指针p指向该数据元素结点,并返回TRUE
//否则指针p指向查找路径上访问的最后一个结点,并返回FALSE
Status SearchBST(BiTree T,int key,BiTree f,BiTree *p)
{
if(!T)//查找不成功
{
*p = f;
return FALSE;
}
else if(key == T->data)//查找成功
{
*p = T;
return TRUE;
}
else if(key < T->data)
{
return SearchBST(T->lchild,key,T,p); //在左子树继续查找
}
else
{
return SearchBST(T->rchild,key,T,p); //在右子树继续查找
}
}//当二叉排序树T中不存在关键字等于key的数据元素时
//插入key并返回TRUE,否则返回FALSE
Status InsertBST(BiTree *T,int key)
{
BiTree p,s;
if(!SearchBST(*T,key,NULL,&p))
{
s = (BiTree)malloc(sizeof(BiTNode));
s->data = key;
s->lchild = s->rchild = NULL;
if(!p) //查找不到key
{
*T = s; //插入s为新的根节点
}
else if(key < p->data)
{
p->lchild = s; //插入s为左孩子
}
else
{
p->rchild =s; //插入s为右孩子
}
}
else
{
return FALSE; //树中有关键字相同的结点,不再插入
//如果想要保存多份相同的可以做个标记
}
}Status DeleteBST(BiTree *T,int key)
{
if(!*T)
{
return FALSE;
}
else
{
if(key == (*T)->data)
{
return Delete(T);
}
else if(key < (*T)->data)
{
return DeleteBST(&(*T)->lchild,key);
}
else
{
return DeleteBST(&(*T)->rchild,key);
}
}
}
Status Delete(BiTree *p)
{
BiTree q,s;
if((*p)->rchild == NULL)
{
q = *p;
*p = (*p)->lchild;
free(q);
}
else if((*p)->lchild == NULL)
{
q = *p;
*p = (*p)->rchild;
free(q);
}
else
{
q = *p;
s = (*P)->lchild;
while(s->rchild)
{
q = s;
s = s->rchild;
}
(*p)->data = s->data;
if(q!=*p)
{
q->rchild = s ->lchild;
}
else
{
q->lchild = s->lchild;
}
free(s);
}
return TRUE;
}平衡二叉排序树
-
如果元素有序,就会生成一个斜二叉树,查找的时间会变长
-
平衡二叉树:要么它是一颗空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1
-
平衡因子:左右子树深度差的绝对值
-
Code
//左子树高
#define LH 1
//左右子树等高
#define EH 0
//右子树高
#define RH -1
typedef struct BiTNode
{
int data;
int bf;//平衡因子
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void R_Roate(BiTree *p)
{
BiTree L;
L = (*P)->lchild;
(*P)->lchild = L->rchild;
L->child = (*p);
*p = L;
}
void LefBalance(BiTree *T)
{
BiTree L,Lr;
L = (*T)->lchild;
switch(L->bf)
{
case LH:
(*T)->bf = L->bf = EH;
R_Rotate(T);
break;
case RH:
Lr = L->rchild;
switch(Lr->bf)
{
case LH:
(*T)->bf = RH;
L->bf = RH;
break;
case EH:
(*T)->bf = L->bf = EH;
break;
case RH:
(*T)->bf = EH;
L->bf = LH;
break;
}
Lr->bf = EH;
L_Roate((*T)->lchild);
R_Roate(T);
}
}
void RightBalance(BiTree *T)
{
}
//taller表示释放长高了
int InsertAVL(BiTree *T,int e,int *taller)
{
if(!*T)
{
*T = (BiTree)malloc(sizeof(BiTNode));
(*T)->data = e;
(*T)->lchild = (*T)->rchild = NULL;
(*T)->bf = EH;
*taller = TRUE;
}
else
{
if(e == (*T)->data)
{
*taller = FALSE;
return FALSE;
}
if(e<(*T)->data)
{
if(!InsertAVL(&(*T)->lchild,e,taller))
{
return FALSE;
}
if(*taller)
{
switch((*T)->bf)
{
case LH:
LefBalance(T);
*taller = FALSE;
break;
case EH:
(*T)->bf = LH;
break;
case RH:
(*T)->bf = EH;
*taller = FALSE;
break;
}
}
}
else
{
if(!InsertAVL(&(*T)->rchild,e,taller))
{
return FALSE;
}
if(*taller)
{
switch((*T)->bf)
{
case LH:
(*T)->bf = EH;
*taller = FALSE;
break;
case EH:
(*T)->bf = RH;
*taller = TRUE;
break;
case RH:
RightBalance(T);
*taller = FALSE;
break;
}
}
}
}
}静态查找和动态查找
-
静态查找:数据集合稳定,不需要添加,删除元素的查找操作
-
动态查找:数据集合在查找的过程中需要同时添加或删除元素的查找操作
-
对于静态查找来说,我们不妨可以用线性表结构组织数据,这样可以使用顺序查找算法,如果我们再对关键字进行排序,则可以使用折半查找算法或斐波那契查找算法等来提高查找的效率
-
对于动态查找来说,我们则可以考虑使用二叉排序树的查找技术,另外我们还可以使用散列表结构来解决一些查找问题
顺序查找
- 顺序查找又叫做线性查找,是最基本的查找技术,它的查找过程是:从第一个(或最后一个)记录开始,逐个进行记录的关键字和给定值进行比较,若某个记录的关键字和给定值相等,则查找成功.如果查找了所有记录仍然找不到与给定值相对的关键字,则查找不成功
折半查找
-
如果待查找的记录是有序的,可以用折半查找
-
折半查找的基本思想:减小查找序列的长度,分而治之的进行关键字的查找
-
折半查找的实现过程:先确定待查找记录的所在范围,然后逐渐缩小这个范围,查找到该记录或查找失败为止
-
Code
int bin_search(int str[],int n,int key)
{
int low,high,mid;
low = 0;
high = n - 1;
while(low <= high)
{
mid = (low + high)/2;
if(str[mid] == key)
{
return mid;
}
if(str[mid]<key)
{
low = mid + 1;
}
if(str[mid] > key)
{
high = mid - 1;
}
}
return -1;
}- 复杂度O(log2n)
插值查找(按比例查找)
-
插值查找就像在查字典的时候,如果单词以a开头,一定会去前面找
-
如果数据变化的比较均匀,差值查找的效率比折半查找的效率高很多,如果不均匀可能会比折半查找慢很多
-
Code
-
Code
int bin_search(int str[],int n,int key)
{
int low,high,mid;
low = 0;
high = n - 1;
while(low <= high)
{
mid = low + (key-a[low]/(a[high]-a[low])*(high-low));
if(str[mid] == key)
{
return mid;
}
if(str[mid]<key)
{
low = mid + 1;
}
if(str[mid] > key)
{
high = mid - 1;
}
}
return -1;
}斐波那契查找(黄金分割查找)
-
黄金比例 0.618:1
-
斐波那契数列(F[k]):1 1 2 3 5 8 13 21 34 55 89 ......
-
比例越来越接近0.612

- Code
#include <stdio.h>
#include <stdlib.h>
#define MAXN 20
/*
*产生斐波那契数列
* */
void Fibonacci(int *f)
{
int i;
f[0] = 1;
f[1] = 1;
for (i = 2; i < MAXN; ++i)
f[i] = f[i - 2] + f[i - 1];
}
/*
* 查找
* */
int Fibonacci_Search(int *a, int key, int n)
{
int i, low = 0, high = n - 1;
int mid = 0;
int k = 0;
int F[MAXN];
Fibonacci(F);
while (n > F[k] - 1) //计算出n在斐波那契中的数列
++k;
for (i = n; i < F[k] - 1; ++i) //把数组补全
a[i] = a[high];
while (low <= high)
{
mid = low + F[k - 1] - 1; //根据斐波那契数列进行黄金分割
if (a[mid] > key)
{
high = mid - 1;
k = k - 1;
}
else if (a[mid] < key)
{
low = mid + 1;
k = k - 2;
}
else
{
if (mid <= high) //如果为真则找到相应的位置
return mid;
else
return -1;
}
}
return 0;
}
int main()
{
int a[MAXN] = { 5, 15, 19, 20, 25, 31, 38, 41, 45, 49, 52, 55, 57 };
int k, res = 0;
printf("请输入要查找的数字:\n");
scanf("%d", &k);
res = Fibonacci_Search(a, k, 13);
if (res != -1)
printf("在数组的第%d个位置找到元素:%d\n", res + 1, k);
else
printf("未在数组中找到元素:%d\n", k);
return 0;
}线性索引查找
-
稠密索引
-
建立和\相同大小的索引表
-
应用于数据量比较小的,如果数据量比较大就必须放在硬盘上,增加了io
-
-
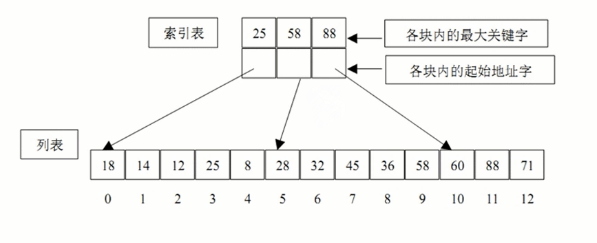
分块索引
- 块内无序,块间有序
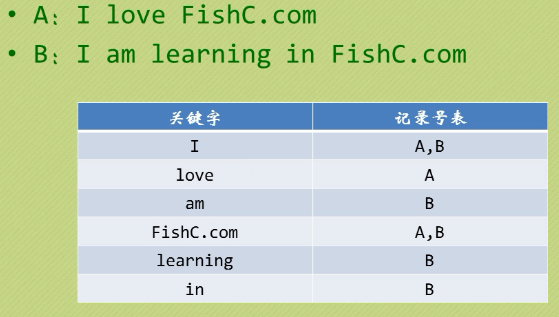
- 倒排索引
二叉排序树
-
无序的顺序表在删除表中的元素的时候可以把后面的元素覆盖待删除的元素,这样效率较高
-
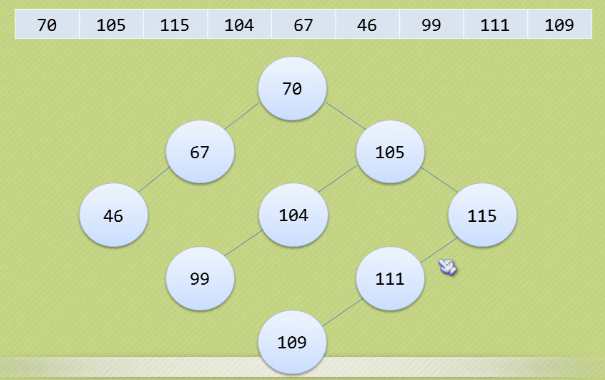
构建二叉排序树:小于根节点的放在左面,大于根节点的放在右边
-
二叉排序树(Binary Sort Tree)又称为二叉查找树,它或者是一颗空树,或者是具有下列性质死亡二叉树:
-
若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值
-
若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值
-
它的左,右子树也分别为二叉排序树(递归)
-
- Code
//二叉树的二叉链表结点结构定义
typedef struct BiTNode
{
int data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;//递归查找二叉排序树 T 中是否存在 key
//指针f指向T的双亲,其初始值调用值为NULL
//若查找成功,则指针p指向该数据元素结点,并返回TRUE
//否则指针p指向查找路径上访问的最后一个结点,并返回FALSE
Status SearchBST(BiTree T,int key,BiTree f,BiTree *p)
{
if(!T)//查找不成功
{
*p = f;
return FALSE;
}
else if(key == T->data)//查找成功
{
*p = T;
return TRUE;
}
else if(key < T->data)
{
return SearchBST(T->lchild,key,T,p); //在左子树继续查找
}
else
{
return SearchBST(T->rchild,key,T,p); //在右子树继续查找
}
}//当二叉排序树T中不存在关键字等于key的数据元素时
//插入key并返回TRUE,否则返回FALSE
Status InsertBST(BiTree *T,int key)
{
BiTree p,s;
if(!SearchBST(*T,key,NULL,&p))
{
s = (BiTree)malloc(sizeof(BiTNode));
s->data = key;
s->lchild = s->rchild = NULL;
if(!p) //查找不到key
{
*T = s; //插入s为新的根节点
}
else if(key < p->data)
{
p->lchild = s; //插入s为左孩子
}
else
{
p->rchild =s; //插入s为右孩子
}
}
else
{
return FALSE; //树中有关键字相同的结点,不再插入
//如果想要保存多份相同的可以做个标记
}
}Status DeleteBST(BiTree *T,int key)
{
if(!*T)
{
return FALSE;
}
else
{
if(key == (*T)->data)
{
return Delete(T);
}
else if(key < (*T)->data)
{
return DeleteBST(&(*T)->lchild,key);
}
else
{
return DeleteBST(&(*T)->rchild,key);
}
}
}
Status Delete(BiTree *p)
{
BiTree q,s;
if((*p)->rchild == NULL)
{
q = *p;
*p = (*p)->lchild;
free(q);
}
else if((*p)->lchild == NULL)
{
q = *p;
*p = (*p)->rchild;
free(q);
}
else
{
q = *p;
s = (*P)->lchild;
while(s->rchild)
{
q = s;
s = s->rchild;
}
(*p)->data = s->data;
if(q!=*p)
{
q->rchild = s ->lchild;
}
else
{
q->lchild = s->lchild;
}
free(s);
}
return TRUE;
}平衡二叉排序树
-
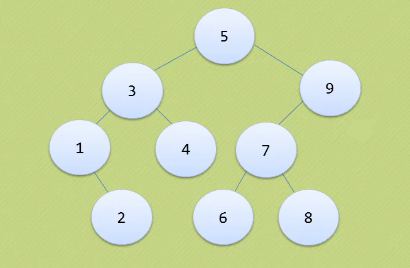
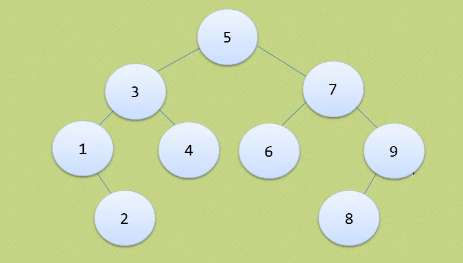
如果元素有序,就会生成一个斜二叉树,查找的时间会变长
-
平衡二叉树:要么它是一颗空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1
-
平衡因子:左右子树深度差的绝对值
- Code
//左子树高
#define LH 1
//左右子树等高
#define EH 0
//右子树高
#define RH -1
typedef struct BiTNode
{
int data;
int bf;//平衡因子
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void R_Roate(BiTree *p)
{
BiTree L;
L = (*P)->lchild;
(*P)->lchild = L->rchild;
L->child = (*p);
*p = L;
}
void LefBalance(BiTree *T)
{
BiTree L,Lr;
L = (*T)->lchild;
switch(L->bf)
{
case LH:
(*T)->bf = L->bf = EH;
R_Rotate(T);
break;
case RH:
Lr = L->rchild;
switch(Lr->bf)
{
case LH:
(*T)->bf = RH;
L->bf = RH;
break;
case EH:
(*T)->bf = L->bf = EH;
break;
case RH:
(*T)->bf = EH;
L->bf = LH;
break;
}
Lr->bf = EH;
L_Roate((*T)->lchild);
R_Roate(T);
}
}
void RightBalance(BiTree *T)
{
}
//taller表示释放长高了
int InsertAVL(BiTree *T,int e,int *taller)
{
if(!*T)
{
*T = (BiTree)malloc(sizeof(BiTNode));
(*T)->data = e;
(*T)->lchild = (*T)->rchild = NULL;
(*T)->bf = EH;
*taller = TRUE;
}
else
{
if(e == (*T)->data)
{
*taller = FALSE;
return FALSE;
}
if(e<(*T)->data)
{
if(!InsertAVL(&(*T)->lchild,e,taller))
{
return FALSE;
}
if(*taller)
{
switch((*T)->bf)
{
case LH:
LefBalance(T);
*taller = FALSE;
break;
case EH:
(*T)->bf = LH;
break;
case RH:
(*T)->bf = EH;
*taller = FALSE;
break;
}
}
}
else
{
if(!InsertAVL(&(*T)->rchild,e,taller))
{
return FALSE;
}
if(*taller)
{
switch((*T)->bf)
{
case LH:
(*T)->bf = EH;
*taller = FALSE;
break;
case EH:
(*T)->bf = RH;
*taller = TRUE;
break;
case RH:
RightBalance(T);
*taller = FALSE;
break;
}
}
}
}
}